Introduction
Linking numerical magnitude to symbolic digits and exploiting associations between magnitude and space are important building blocks of arithmetic knowledge. Cognitive psychologists have developed experimental paradigms for the investigation of magnitude and spatial representations in a numerical context (Moyer and Landauer, 1967; Henik and Tzelgov, 1982; Dehaene et al., 1993). Recent studies have exploited these experimental paradigms in order to specify early developmental changes in the magnitude (e.g., Girelli et al., 2000; Rubinsten et al., 2002) and spatial (Berch et al., 1999; van Galen and Reitsma, 2008) representation of number in children. However, to date no studies examined the concurrent development of magnitude and spatial representations within the same population of children. In order to fill this gap here we provide a study of integrating magnitude and spatial information with symbolic number knowledge in a single population of children in Years 1–3 of primary school. Further, we have increased experimental power over previous studies and used a sensitive measure of magnitude processing (the distance effect with task-irrelevant numerical information) so that discrepancies between previous experimental literature and preceding developmental theories could be reconciled (Resnick, 1983; Case and Griffin, 1990; Fuson and Briars, 1990; Griffin and Case, 1996; Okamoto and Case, 1996; Griffin, 2004, 2005).
According to the model of Dehaene and Cohen (1995) human arithmetic skills rely on an extended network of mental representations. It is thought that one of these representations is an analog-like magnitude representation (Dehaene, 1997), which enables the understanding of numerical relations when comparing quantities and it is thought to provide a pre-symbolic foundation of numerical knowledge that remains functional after the acquisition of symbolic representations (Moyer and Landauer, 1967). Further, it is often thought that this magnitude representation also becomes spatially organized, being similar to a mental number line (e.g., Schneider et al., 2009). In fact, it is often implied in the literature that magnitude interpretation and the number line are implemented by the same representation. However, this is not the case: magnitude and spatial information are represented independently; spatial associations with magnitude information are culturally determined and are related to the direction of writing learnt in school and are not part of any core magnitude representation (Shaki et al., 2009). Hence, linking symbolic digits to analog magnitude and associating symbolic digits and magnitude with spatial information reflect different processes. In fact, the development of magnitude and spatial information has been investigated in separate studies so far.
The overwhelming majority of experimental studies tracked the development of the magnitude representation. The core signature of the magnitude representation, which is present from infancy (Xu and Spelke, 2000; Feigenson et al., 2002), is that it is harder to discriminate quantities when their ratio is closer to one (e.g., 2 and 3), relative to the ratio being further away from one (e.g., 1 and 5). In the domain of symbolic numbers the most researched expression of the ratio “rule” is the numerical distance effect (Moyer and Landauer, 1967; Holloway and Ansari, 2009) which is frequently considered to be a marker of automatic magnitude processing. However, it has been suggested that distance effects in intentional paradigms reflect the properties of comparison processes and/or stimulus/response associations rather than properties of the magnitude representation (van Opstal et al., 2008; van Opstal and Verguts, 2011). Therefore, intentional measures are not appropriate to determine the properties of the number representation and related developmental effects with certainty (for a detailed discussions see Rubinsten et al., 2002; Tzelgov and Ganor-Stern, 2005). In contrast, if the magnitude information can be shown to be activated in an automatic fashion, it can be assumed that it forms an inherent component of the representation of symbolic numbers.
A particularly popular paradigm allowing for the study of automatic access to the magnitude representation is the so-called numerical Stroop paradigm (NSP; Henik and Tzelgov, 1982). In the NSP, participants are asked to compare simultaneously presented Arabic digits based on either their physical or numerical magnitude (Table 1). In the physical comparison task, numerical information is irrelevant yet adults consistently slow down when there is a mismatch between the relevant and irrelevant dimensions, this is called the congruity effect (e.g., Henik and Tzelgov, 1982; Tzelgov et al., 1992; Girelli et al., 2000; Rubinsten et al., 2002; Kaufmann and Nuerk, 2006; Mussolin and Noël, 2007; Rousselle and Noël, 2007, 2008; Szücs and Soltész, 2007; Szücs et al., 2007; Gebuis et al., 2009; Landerl and Kölle, 2009).
Using the NSP with symbolic digits Girelli et al. (2000) found the congruity effect in children in Grades 3 (aged 8 years 4 months) and 5 (10 years 3 months) but not in Grade 1 (6 years 6 months). In contrast, Rubinsten et al. (2002) found the congruity effect at the end of Grade 1 (7.32 ± 0.43 years) but not at the beginning of Grade 1 (6.25 ± 0.43 years). Rousselle and Noël (2008) used the physical comparison task of a non-symbolic (dot discrimination) NSP with 4, 5, and 6 year olds. There were significant congruity effects in all age groups. Gebuis et al. (2009) tested 5 year olds in the physical comparison task of the NSP with both non-symbolic and symbolic representations and reported the congruity effect with non-symbolic but not with symbolic stimuli which suggests that 5-year-old children do not yet integrate magnitude with symbolic digits.
With regard to the distance effect, none of the above behavioral studies reported significant distance effects in the physical comparison task of the NSP. This is a shortcoming from the point of view that Stroop congruency is strongly affected by the development of response inhibition, hence, the size of the congruency effect cannot serve as a pure marker of the developmental level of automatic magnitude access (Szücs et al., 2007; Szűcs et al., 2009; Bryce et al., 2011). Further, as proposed by Tzelgov et al. (1992) while the presence of Stroop congruency effects certainly suggests automatic processing of digits, it does not suggest that a refined evaluation (going beyond small/large categories) happens. In contrast, the presence of distance effects in the physical comparison task of the NSP would suggest more refined magnitude processing. Adult studies found evidence for this (e.g., Henik and Tzelgov, 1982; Szücs and Soltész, 2007; Szücs et al., 2007). For example, Henik and Tzelgov (1982) reported that in the incongruent condition of the physical size decision numerical Stroop task pairs with task-irrelevant large numerical distance were slower to be compared than pairs with small numerical distance. In contrast, a distance effect with an opposite pattern appeared in the congruent condition. This significant interaction can be taken as an indicator of refined numerical processing, and warrants developmental investigation. Hence, measuring distance effects and their interaction in the Stroop paradigm is advantageous for two reasons. First, the automatic distance effect is probably a more pure measure of automatic access to the magnitude representation than Stroop congruency. Second, distance effects could provide behavioral evidence for refined automatic magnitude processing. It is to note that in contrast to the lack of previous behavioral evidence electro-physiological studies have demonstrated that distance effects in the NSP occur with similar speed (200 ms after stimulus presentation) in children (Grades 1, 2, 3, and 5) and adults (Szücs et al., 2007; Soltész et al., 2011). Similarly to congruity effects, these results confirm that the extraction of numerical information from digits becomes highly automatic during early school years. This can have functional relevance, for example, Griffin et al. (1995) suggest that increased automaticity underpins the acquisition of calculation skills during arithmetic development.
With regard to the role of spatial representations in number knowledge there is considerable evidence for a connection between visuo-spatial and numerical information in adults (see Fias and Fischer, 2005 for review). The most popular experimental measure is the spatial–numerical association of response codes (SNARC) effect introduced by Dehaene et al. (1993). The SNARC effect is typically elicited in parity judgment tasks because they do not require conscious magnitude or spatial processing. Typically, faster response times are observed when small numbers correspond to the left hand side than the right hand side, with the converse relationship holding true for larger numbers. Findings are usually attributed to the development of an associative link between number and space, with the processing of number automatically activating a spatially oriented, culturally defined mental number line (Dehaene et al., 1993; Fias and Fischer, 2005). The implicit testing of spatial information is a significant difference between SNARC and number line studies (Siegler and Opfer, 2003; Siegler and Booth, 2004; Booth and Siegler, 2006; Ebersbach et al., 2008; Schneider et al., 2009), which ask for explicit access to spatial and magnitude information related to numbers (see above about the relevance of automaticity). Recently, it has been questioned whether the SNARC effect directly reflects representational properties (van Dijck and Fias, 2011) as it was demonstrated that the SNARC effect is based on actual coding of information in working memory rather on the number representation. However, even if this is the case it seems that the effect can still be used for characterizing the “default” coding of spatial–numerical information (i.e., the immediate SNARC effect may reflect an effective “default” coding of numbers based on long-term memory spatial–numerical associations).
Despite the fact that the SNARC effect seems to reveal an important property of the symbolic number representation, surprisingly little is known about its development. Berch et al. (1999) have investigated the SNARC effect with child participants (Grades 2, 3, 4, 6, and 8; Mean age: 7.8, 9.2, 9.8, 11.7, and 13.6 years). This study concluded that children did not show the SNARC effect until Grade 3 (9.2 years) and that the effect was attenuated in sixth and eighth graders. The failure of Grade 2 (7.8 years) children to demonstrate the SNARC effect during the parity judgment task was attributed to high RT variability and generally slower response (Berch et al., 1999). While this could be a valid claim, design factors could also have contributed to detecting a relatively late onset of the SNARC effect. First, digits 0–9 were presented, yet only 0, 1, 8, and 9 were used in analysis; with the parity judgment of 0 not a typical task for children. Furthermore, the design did not encourage a speeded, automatic response, and participants received no feedback on their performance. Any of these factors could have been responsible for the slower and varied RTs reported in the study. Subsequently, by building on the work of Berch et al. (1999), there is a chance that the SNARC effect could be observed developmentally earlier than 9.2 years of age.
The only other developmental SNARC study to date utilized an alternative paradigm with children aged 7, 8, and 9 years (van Galen and Reitsma, 2008). This study employed two scenarios: number magnitude being relevant or irrelevant. One task was a standard number comparison task (number magnitude relevant) and the other was a detection task, similar to that adopted by Fischer et al. (2003), that required children to identify a left or right target after observing a number (number magnitude irrelevant). When number magnitude was relevant there was a significant SNARC effect for all children (7, 8, and 9 years). In contrast, only from 9 years of age was the SNARC effect significant when number magnitude was irrelevant. It was argued that this age demonstrates the onset of automatic access to spatial information represented by symbolic digits. van Galen and Reitsma’s (2008) automatic SNARC effect at approximately 9 years of age is aligned with the parity judgment task of Berch et al. (1999); however, it could be questioned as to whether the task (van Galen and Reitsma, 2008) had a chance to elicit a genuine spatial–numerical association in all child groups. Success in the magnitude irrelevant task was dependent on identifying a peripheral target, not the presented digits and therefore it is unclear whether younger children attended to the number at all. The alternative paradigm of Berch et al. (1999), where magnitude was irrelevant, but where children were required to process stimuli along another numerical dimension is more in line with the usual SNARC setup used in adult research (Dehaene et al., 1993).
Besides the above studies based on the numerical Stroop and SNARC effects several authors proposed to use the term “central conceptual structure” of number (e.g., Siegler and Robinson, 1982; Resnick, 1989; Fuson and Briars, 1990; Dennis, 1992; Geary, 1994; Okamoto and Case, 1996; Griffin, 2004, 2005) building on cognitive development theories (e.g., Piaget, 1952; Gelman and Gallistel, 1978; Carey, 1985). According to the above theorists the central conceptual structure can be defined as a network of semantic representations/nodes and their connections/relations. The integration of various representations into a complex representational network (a central conceptual structure superordinate to individual representations) is a necessary prerequisite of a complex, culturally developed representation of number and hence, of adequate numerical competence (Fuson and Briars, 1990; Griffin and Case, 1996; Okamoto and Case, 1996; Griffin, 2004, 2005). On the basis of several observations these theories generally assumed that quantity integrates into the central conceptual structure of number at approximately 5–6 years of age, and these representations are then linked to formal symbols at around 6–7 years of age (Fuson and Briars, 1990; Okamoto and Case, 1996; Griffin, 2004). Further, number line studies suggest that accuracy in translating quantity to a spatial representation appears to develop later at 7–8 years of age (Siegler and Opfer, 2003; Siegler and Booth, 2004; Booth and Siegler, 2006). These findings point toward magnitude and spatial information integrating sequentially into a central conceptual structure of number within the 6- to 8-years timeframe. This putative timeline, however, is not directly aligned with the experimental evidence that delays these milestones to approximately 7 years for automatic extraction of magnitude information from Arabic digits (Rubinsten et al., 2002) and approximately 9 years for an automatic SNARC effect (Berch et al., 1999; van Galen and Reitsma, 2008).
Our study was motivated by two objectives. First, so far no study investigated the developmental timeline of integrating numerical magnitude and spatial information into the central conceptual structure of number within a single population of children in Years 1, 2, and 3 of primary school. Second, as noted above, there are inconsistencies between the developmental timelines proposed by Stroop/SNARC and other studies. We used two experimental tasks. In task 1, we measured automatic access of semantic information by using a physical size decision numerical Stroop task. We not only examined congruency effects but also the effect of task-irrelevant numerical distance as these seem to be a more reliable measure of magnitude activation from symbolic digits as explained above. In task 2, we examined the automatic access to spatial–numerical information. We increased the power of previous examinations and thus expected to be able to detect an earlier SNARC effect than previous investigators. Our core question was to detect the timeline of involuntarily activation of numerical magnitude and spatial information when children encounter symbolic numerical information. Importantly, none of the above tasks required explicit activation of numerical magnitude or spatial knowledge. Hence, experimental effects cannot be attributed to intentional effects, rather, they probably reflect the automatic activation of magnitude information and the default coding of spatial–numerical information.
Materials and Methods
Participants
Sixty-five British children from Years 1, 2, and 3 (Year 1: n = 21, mean age 6.2 ± 0.29 years, 9 females; Year 2: n = 19, mean age 7.5 ± 0.42 years, 13 females; Year 3: n = 25, mean age 8.5 ± 0.35 years, 10 females) formed the participant pool. All children were typically developing and had no learning difficulties. Parental informed written consent was obtained for all participants. The study received ethical approval from the Psychology Research Ethics Committee.
Task 1: Automatic Access to Magnitude Information
Stimuli were two single-digit numerals, presented on a 19″ computer monitor with black background and white digits in Times New Roman font. The digit pairs were constructed from the numbers 1, 2, 8, and 9 (NB: the same digits were also used in Task 2). There were three numerical distances: 1 unit (the digits 1–2, 2–1, 8–9, and 9–8), 7 units (the digits 1–8, 8–1, 2–9, and 9–2), or 0 units (the digits 1–1, 2–2, 8–8, and 9–9). The physical size attribute had three size variations 40, 45, and 50 points. There were two physical differences: a small difference (sizes 40–45pt, 45–40pt, 45–50pt, and 50–45pt) and a large difference (sizes 40–50pt and 50–40pt). A congruent stimulus was defined as a pair of digits in which a given digit was larger on both the numerical and physical dimensions (e.g., 8 1). An incongruent stimulus was defined as a pair of digits in which a given digit was simultaneously larger in physical size and smaller in numerical size (e.g., 1 2). A neutral stimulus was defined as a pair of digits that differed only in physical size (e.g., 2 2).
Each trial began with a fixation sign (the drawing of an eye) shown for 300 ms which was followed by a delay of approximately 1000 ms. This was followed by the stimulus for 3000 ms (or until response), then a 1000-ms inter trial interval. In half of the trials the physically larger number appeared on the right, in the other half, on the left. The same held for the position of the numerically larger number as well. Congruency, physical distance, numerical distance, and the side of the response (left or right hand) were manipulated orthogonally.
The participants’ task was to press the left or right button that corresponded to the physically larger of the digit pairs as quickly and accurately as possible. Given the presentation of all congruency conditions and the counter balancing of response side, there were 48 digit pairs per block. These pairs appear in a pseudo random order, controlling for the same stimuli appearing twice in succession. Given the age of the children, the task contained one practice block (24 trials) and three or four testing blocks depending on the comfort of the child. That is, each stimulus appeared 24 or 32 times, depending on whether three or four testing blocks were presented.
Mean accuracy and median RTs were calculated and used in statistical analyses for individuals. In order to investigate the size congruity effect, for both accuracy and RT data, a 3 × 3 × 2 × 2 mixed design ANOVA was run. Factors were: Year (Year 1, 2, and 3) × Congruency (Congruent, Incongruent, and Neutral) × Physical Distance (small 5pts, large 10pts) × Numerical Distance (1 unit, 7 units). Year group was a between subjects factor, congruency, physical, and numerical distance were within-subjects factors. Following the method of Rubinsten et al. (2002) half of the trials in the neutral condition were randomly assigned to the small numerical distance, and the other half to the large numerical distance condition.
To investigate the influence of the irrelevant numerical distance dimension and the refined automatic processing of magnitude information, we conducted a separate 3 × 2 × 2 × 2 ANOVA on data from the congruent and incongruent conditions only. The neutral condition was removed in this analysis because numerical distance was by definition zero. Factors were: Year (Year 1, 2, and 3) × Congruency (Congruent, Incongruent) × Physical Distance (small, large) × Numerical Distance (1 unit, 7 units). Due to the focus on developmental trends and for coherence with existing studies (Girelli et al., 2000; Rubinsten et al., 2002), all ANOVAs were also conducted as separate year group analyses. All post hoc analyses were Tukey HSD tests.
Task 2: Automatic Access to Spatial Information
Participants made parity judgments of single-digit numbers. Stimuli were distinctly small (1, 2) and large single-digit numbers (8, 9) presented on a 15.4″ screen laptop with black background and white digits in 40pt Times New Roman font. Participants were instructed to decide whether the digits were odd or even. Responses were made using two buttons, allocated to the left and right side of the keyboard and were labeled “odd” and “even,” and accordingly there were two alternative response conditions (Left-Odd and Right-Odd). The order of the different response conditions (Left-Odd first or Right-Odd first) was counterbalanced for each year level.
Each trial began with a fixation sign (the drawing of an eye) shown for 300 ms which was followed by a delay of approximately 1000 ms. This was followed by the stimulus for 3000 ms (or until response), then a 500-ms inter trial interval. Each response condition (Left-Odd and Right-Odd) consisted of three blocks of 20 trials (120 trials in total), with each stimulus appearing 30 times (15 left response and 15 right response). A practice block of 12 trials preceded each response condition. Stimuli were presented in a pseudo random order and participants were encouraged to be both accurate and fast in their response. Participants received performance feedback after each block. Prior to completing the parity judgment task, all children completed a familiarization activity related to the parity (odd–even classification) of digits 1–10. The behavioral measures commenced when children were able to successfully identify odd–even classifications during a verbal assessment.
Mean accuracy and median RTs were calculated and used in statistical analyses for individuals. Initially, a 3 × 2 × 2 mixed design ANOVA was run. Factors were: Year group (Year 1, 2, and 3) × Magnitude (small, large numbers) × Response side (left, right). Year group was a between subjects factor, magnitude, and response side were within-subjects factors. “Small” numbers were 1 and 2 and “large” numbers were 8 and 9. With the SNARC effect representing a behavioral response that arises from corresponding number magnitude and spatial location, throughout the analysis the SNARC effect was defined as the interaction between magnitude and response side dimensions. Separate year group analyses were conducted and all post hoc analyses were Tukey HSD tests.
In order to examine the potential interrelationships between Stroop and SNARC effects at the individual level congruency (accuracy and RT) and SNARC (accuracy and RT) variables were entered into a partial correlation, controlling for age and IQ. The congruency variables (accuracy and RT) were calculated by the following equation: (|neutral − congruent| + |incongruent − neutral|)/2. The SNARC variables (accuracy and RT) were calculated with the following equation: (|small right − small left|+|large left − large right|)/2. There were six relevant correlations between these variables. Hence, in order to correct for multiple comparisons a Bonferroni correction was applied and effects at an alpha level of p < 0.05/6 < 0.0083 were considered significant.
Results
Task 1: Automatic Access to Magnitude Information
Congruity effect
Overall. Overall and group means for accuracy and medians for RT are given in Table 2. For overall measures of accuracy there was a main effect of year [F(2, 62) = 8.155, p < 0.001] and post hoc analysis indicated that this was driven by Year 1 accuracy (69 ± 19%) being significantly lower than both Year 2 (79 ± 16%) and Year 3 (83 ± 14%). As expected there was also a main effect of congruency [F(2, 124) = 169.406, p < 0.001]. Post hoc comparisons revealed that it was the accuracy of incongruent condition that was significantly lower than both congruent and neutral conditions, however, congruent and neutral conditions were similar (Table 2). The interaction Congruency × Year was significant [F(4, 124) = 4.541, p = 0.002], but post hoc analysis indicated this was driven by differences within year groups. For example, within each year group there were significant differences between the congruent and incongruent conditions, as well as the incongruent and neutral conditions. The only between group differences where in comparison to Year 1 but these were across different congruency conditions. For example, Year 1 incongruent accuracy was significantly different to the Year 2 neutral condition and the Year 3 congruent condition.
In overall RT measures there was a main effect for congruency [F(2, 124) = 74.380, p < 0.001] but not year. Post hoc comparisons revealed that it was the RT of the incongruent condition that was significantly slower than that of both congruent and neutral conditions, which were similar (Table 2). The interaction Congruency × Year was not significant (F < 1, p = 0.93).
Separate year group analyses. The statistical results showed similar significant congruency effects for both accuracy and RT (ps < 0.001). This was also maintained throughout the post hoc analyses, in that all significant differences were between the incongruent and congruent (ps < 0.001) and the incongruent and neutral (ps < 0.001) conditions; neutral and congruent conditions were not significantly different.
Influence of irrelevant numerical distance on congruency
Overall. On its own, the irrelevant numerical distance dimension (1 and 7 unit differences) did not demonstrate a significant main effect in either accuracy or RT (F < 1, p = 0.56; F < 1, p = 0.44, respectively). In accuracy, both numerical distances had accuracy scores of approximately 75% (1 unit difference: 75 ± 19%; 7 unit difference: 75 ± 17%). The 1 and 7 unit numerical distances demonstrated similar RT behaviors with 686 ± 85 and 684 ± 88 ms, respectively.
Importantly, for the purposes of examining refined automatic processing of magnitude information, the irrelevant numerical distance did interact with congruency. In accuracy there was a significant Congruency × Numerical Distance interaction [F(1, 62) = 39.515, p < 0.001] that indicated a reversal of the traditional distance effect. This was categorized by higher accuracy in the congruent condition when corresponding to a small numerical distance (84 ± 15%), in comparison to a large numerical distance in the congruent condition (78 ± 17%).
Separate year group analyses. Results for accuracy are depicted in Figure 1. Planned comparisons demonstrated the Congruency × Numerical Distance interaction was significant across all year levels [Year 1: F(1, 20) = 10.376, p = 0.004; Year 2: F(1, 18) = 7.741, p = 0.001; Year 3: F(1, 24) = 26.372, p < 0.001]. Post hoc analyses indicated there was a significant numerical distance effect in Years 1–3, in both congruent and incongruent conditions (ps < 0.001). In all groups there was a reverse distance effect in the congruent condition, with the small numerical distances (1 unit) responded to more accurately than the larger numerical distances (7 units). Meanwhile, there was a traditional distance effect in the incongruent condition. In RT the Congruency × Numerical Distance interaction was not significant [F(1, 62) = 1.392, p = 0.243].
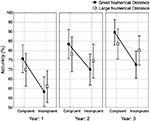
Figure 1. Developmental trends, by year group, of Congruency × Numerical Distance, for accuracy. The error bars indicate 95% confidence intervals.
Task 2: Automatic Access to Spatial Information
Overall
Overall and group means for accuracy and medians for RT are given in Table 3. In accuracy, there was a significant main effect for year [F(2, 62) = 8.28, p < 0.001], with post hoc analyses indicating that Year 1 accuracy of 86 ± 9% was significantly lower than both Year 2 (92 ± 8%) and Year 3 (93 ± 6%) accuracy scores (ps < 0.01). Furthermore, for accuracy there was a significant SNARC effect [Magnitude × Response Side: F(1, 62) = 10.22, p = 0.002]. This effect appeared because small numbers were responded more accurately with the left hand than with the right hand (difference 3%, Table 3, p = 0.02) and simultaneously, large numbers were responded to more accurately by the right hand, in comparison to the left hand (difference 2%, Table 3, p = 0.32).
RT data indicated main effects for both magnitude [F(1, 62) = 11.695, p = 0.001] and year [F(2, 62) = 7.868, p < 0.001]. For the main effect of magnitude, large numbers produced longer RTs (1101 ± 255 ms) than small number magnitudes (1063 ± 227 ms). For the main effect of year, post hoc analysis indicated that the RTs of Year 1 children (1229 ± 260 ms) were significantly slower than the RTs of Year 2 (1032 ± 211 ms) and Year 3 (997 ± 188 ms; ps < 0.01). In RT the SNARC effect (Magnitude × Response Side) was also significant [F(1, 62) = 8.58, p = 0.003]. The interaction appeared because large numbers were responded 47 ms faster with the right hand than with the left hand (p = 0.02) whereas small numbers were responded to 22 ms faster with the left hand than with the right hand (p = 0.49; Table 3).
Separate year group analyses
Graphical results for accuracy are in Figure 2. In the planned comparisons for accuracy, Year 1 children were the only group to show a response side bias [F(1, 20) = 8.217, p = 0.010]. These findings were potentially driven by the right side response accuracy of 84 ± 9% being lower than the 87 ± 9% accuracy of the left side in the Year 1 participants. No year group demonstrated a main effect of number magnitude (Fs < 1). A developmental progression became evident with the SNARC effect (Magnitude × Response Side) for accuracy not significant in Year 1 [F(1, 20) = 1.528, p = 0.231] or Year 2 [F(1, 18) = 2.401, p = 0.139], but reaching significance in Year 3 [F(1, 24) = 8.52; p = 0.008; Figure 2].
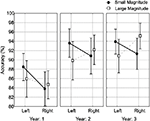
Figure 2. The SNARC effect (Magnitude × Response Side) for accuracy; the effect was significant in Year 3. The error bars indicate 95% confidence intervals.
Graphical representations of the separate year group results for RT are in Figure 3. Firstly, no year group demonstrated a significant response side bias. Both Years 2 and 3 did produce significant magnitude effects [Year 2: F(1, 18) = 4.711, p = 0.044; Year 3: F(1, 24) = 8.210; p = 0.009], whereas Year 1 children did not [F(1, 20) = 2.802; p = 0.110]. In both Years 2 and 3, this significant effect was characterized by small digits having a faster RT (Year 2: 1015 ± 197 ms, Year 3: 980 ± 176 ms) than larger digits (Year 2: 1049 ± 226 ms, Year 3: 1013 ± 200 ms). In contrast to the accuracy results, RT behaviors demonstrated a significant SNARC effect (Magnitude × Response Side) in Years 2 and 3 [Year 2: F(1, 18) = 4.783; p = 0.042; Year 3: F(1, 24) = 9.456; p = 0.005], but not in Year 1 (F < 1; Figure 3).
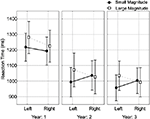
Figure 3. The SNARC effect (Magnitude × Response Side) for RT; the effect was significant in Years 2 and 3. The error bars indicate 95% confidence intervals.
None of the partial correlations between Stroop and SNARC task variables were significant.
Discussion
Our study examined the developmental timeline of the integration of both magnitude and spatial information with symbolic numbers within a single group of Year 1–3 primary school children. Automatic access to magnitude information was tested by the physical size decision task of the NSP. Automatic access to spatial information was tested by a parity judgment task. These tasks did not require overt numerical magnitude and spatial analysis. Hence, any effects of magnitude and spatial information can be taken as evidence that magnitude and spatial information becomes an inherent property of the representation of symbolic number.
In the physical size decision Stroop task all groups of children, Years 1, 2, and 3, demonstrated the congruity effect for both accuracy and RT measures. This finding demonstrates that children as young as 6.2 ± 0.29 years can automatically access magnitude information represented by symbolic digits. Previously, the earliest observation of the symbolic congruity effect was more than a full chronological year later than our results, at the end of Grade 1 with participants aged 7.3 ± 0.43 years (Rubinsten et al., 2002), with Szücs et al. (2007) and Girelli et al. (2000) determining the effect in Grade 3. In previous studies, using non-symbolic comparison tasks, the congruity effect was observed in children as young as 4 years of age (Rousselle and Noël, 2008; Soltész et al., 2010). However, the symbolic modality is more informative for application to an educational context. Similarly to Rubinsten et al. (2002) we interpret the findings to suggest that it is the period of formal education that counts toward the development of the symbolic congruity effect, not years of age. Rubinsten et al. (2002) argued that by the end of the first year of formal education, children had enough exposure to Arabic digits that they were able to demonstrate a symbolic congruity effect. The present results support this assertion and extend the argument with the fact that children of a younger chronological age, yet the same years of education can demonstrate the same access to symbolic representations. From this point of view it would be very interesting to study whether differences in the onset of congruency effects are influenced by different education systems in various countries.
In the physical size decision Stroop task we not only tested the congruity effect but also analyzed numerical distance effects evoked by task-irrelevant numerical meaning of symbolic digits. This analysis was motivated by the work of Tzelgov et al. (1992) who argued that the congruity effect alone was a marker of rough categorization (e.g., small/large) of the irrelevant numerical dimension; whereas the Congruency × Numerical Distance modulations suggest that a refined representation of magnitude is accessed automatically. In our study children demonstrated significant Congruency × Numerical Distance interaction in accuracy and post hoc tests revealed significant distance effects in both the congruent and incongruent conditions. A significant Congruency × Numerical Distance interaction has previously been observed in RT in adults (Henik and Tzelgov, 1982; Szücs et al., 2007) and a statistically non-significant reversed distance effect was reported in accuracy in Grade 5 children (Girelli et al., 2000). The adult reverse distance effects (Henik and Tzelgov, 1982; Szücs et al., 2007) were typically expressed in the incongruent condition. This significant effect in adults was characterized by small numerical distances resulting in a faster response than the large numerical distances, within the incongruent condition. The present child participants from Year 1 (6.2 ± 0.29 years) through to Year 3 (8.5 ± 0.35 years) demonstrated more accurate responses in the congruent condition when the numerical distance was small, in comparison to large numerical distances.
While detecting a modulation of congruity effects by task-irrelevant numerical distance is highly significant on its own (Tzelgov et al., 1992), actual speed and accuracy outcomes in the NSP may not be straightforward to explain because exact values depend on the relative saliency and speed of processing of task-relevant and task-irrelevant dimensions as well as on the ability to resolve stimulus and response conflict in the incongruent condition (Boucart and Humphreys, 1994; Schwarz and Ischebeck, 2003; Szücs and Soltész, 2007; Szücs et al., 2007; Szűcs et al., 2009). This means that the comparison of specific reaction time and accuracy outcomes across studies may be difficult because actual stimulus parameters greatly influence these dependent variables. For example, it is probable that in our study when children were slowed down by conflict in the incongruent condition they had more time to access numerical information which may than have mislead children to focus on the numerical dimension either voluntarily or involuntarily in a small proportion of trials. If children made numerical rather than physical size decisions in these few trials that was counted as an error. Hence, a standard, overt decision-related numerical distance effect may have appeared, that is, more errors were committed in the small than in the large numerical distance condition. This explains the normal numerical distance effect in the incongruent condition. In contrast, in the congruent condition children were not slowed down by conflict and they made a physical judgment. Hence, children were not misled to make numerical comparisons in some trials. That is, the more overlapping neural representations of the magnitude linked to symbolic digits in the small relative to the large distance condition (e.g., the neural representations of 2 and 3 and more overlapping than that of 2 and 8) supported physical judgments more in the small than in the large distance condition (Dehaene et al., 1998; Szücs and Soltész, 2007). This can explain the reversed distance effect in the congruent condition. Further, while adults typically did not show reverse distance effects in accuracy (Henik and Tzelgov, 1982; Szücs et al., 2007), and their reverse distance effect pattern in reaction time can be explained by for example the relative speed account of Schwarz and Ischebeck (2003). Importantly, the different nature of reversed distance effects in adults and children and the fact that these phenomena show up in different measures suggests that the details of these effects may have different explanations in adults and children which could be clarified by future research.
Our second task investigated the development of the automatic access to spatial information represented by digits in a parity judgment task. On the basis of developmental research (Griffin and Case, 1996; Griffin, 2005) we hypothesized that children should demonstrate the integration of spatial directions and symbolic number soon after the acquisition of formal symbols at approximately 6–7 years of age (i.e., approximately Year 2). Results were in agreement with our expectations: The SNARC effect was observed in RT in Year 2 British children, with a mean age of 7.5 ± 0.42 years, more than two years younger than the 9.8-year-old Grade 3 US participants reported in the Berch et al. (1999) study. The increased sensitivity of our task can probably be attributed to having a larger number of trials using more distinct digits in comparison to Berch et al. (1999). Similarly, our results show earlier onset of the SNARC effect than in the study of van Galen and Reitsma (2008) who observed this onset in 9.2-year-old Grade 3 Dutch children in a task where number meaning was irrelevant. van Galen and Reitsma (2008) also used another, explicit number comparison task where number meaning was relevant and in that case they reported the onset of the SNARC effect in Grade 1 (7.0-year-old) children. However, this result should be interpreted cautiously as adult SNARC research usually avoids using tasks which require explicit activation of the magnitude representation because magnitude it more readily accessed than parity (Dehaene et al., 1993) and therefore findings may not adequately characterize automatic access to spatial–numerical information. Because a magnitude comparison task (van Galen and Reitsma, 2008) requires explicit attention on number magnitude, the observed voluntary SNARC effect cannot be considered to reveal an inherent property of symbolic numbers. The parity judgment task used in the present study required the semantic processing of the number symbol, but not directly the magnitude or spatial information. As noted in the introduction, even if the SNARC effect is vulnerable to actual working memory coding of information (van Dijck and Fias, 2011), our results suggest that by the second year of school spatial–numerical associations solidify in children’s learn long-term memory, hence, children use these associations for the effective default coding of numerical information in a task situation.
It is worth noting that in the SNARC task Year 2 and 3 children displayed a magnitude effect for RT (slower RT for larger magnitudes), while the Year 1 group did not. This could indicate various developmental trends. First, Berch et al. (1999) thought this magnitude effect was an indication of an attempt at strategy implementation, such as dividing by two, that could be slowing RT. Second, it could be related to the understanding of the parity judgment task itself. It is proposed that for children in Years 2 and 3, the difficulty and/or confidence in parity judgment with larger magnitudes could influence and increase RTs for larger digits, thus facilitating the magnitude effect. This explanation cannot extend to the Year 1 children, and given that these participants also demonstrated a response side bias for accuracy means that the Year 1 results should be interpreted carefully.
For the first time, we have tested a single population of Year 1, 2, and 3 children to investigate how both magnitude and spatial information integrate with the knowledge of symbolic digits. Our research connects experimental (Berch et al., 1999; Girelli et al., 2000; Rubinsten et al., 2002; van Galen and Reitsma, 2008) and traditional developmental (Resnick, 1983; Case and Griffin, 1990; Fuson and Briars, 1990; Griffin and Case, 1996; Okamoto and Case, 1996; Griffin, 2004, 2005) literature. Our data suggest that in Year 1 (6.2 ± 0.29 years) children are accessing the symbolic representation of number, as indicated by the symbolic congruity effect. At this stage the association between the magnitude and symbolic representations is to the point where irrelevant numerical distance can modulate congruency effects (Congruency × Numerical Distance). Because of the nature of the physical size judgment task of the NSP, this distance effect can be considered a marker of refined automatic symbolic number analysis from Year 1 onward (6.2 ± 0.29 years). This finding extends the prior research of De Smedt et al. (2009), Holloway and Ansari (2008), and Sekuler and Mierkiewicz (1977) who determined a distance effect in 6-year-old children via an overt number comparison task. In addition, testing for the SNARC effect has determined that Year 2 (7.5 ± 0.42 years) marks the onset of the spatial–numerical association of number and space in relation to numerical symbols. The current findings support a sequential integration of magnitude and spatial information with the concept of symbolic digits. This first begins with a semantic magnitude association, revealed via Stroop congruity and involuntary distance effects, and then develops to include a spatial association as shown by the SNARC effect. The above sequential process of integration is evidenced by the fact that Year 1 children demonstrated the congruity effect and involuntary distance effects, but not yet the SNARC effect. The lack of correlations between Stroop and SNARC effects suggests that the integration of magnitude and spatial information with the concept of symbolic digits is fairly independent. Further investigations that extend the present findings could prove insightful about the development of arithmetic competence during formal schooling, as it was earlier identified by Griffin et al. (1995) that such automaticity with Arabic digits could be linked to the acquisition of calculation skills and the understanding of visuo-spatially represented functions.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This research was conducted as part of the PhD project completed by Sonia White at the University of Cambridge, supported by the Cambridge Commonwealth Trust. Writing up the project benefited from support from a grant from the Medical Research Council (G90951).
References
Berch, D. B., Foley, E. J., Hill, R. J., and Ryan, P. M. (1999). Extracting parity and magnitude from Arabic numerals: developmental changes in number processing and mental representation. J. Exp. Child Psychol. 74, 286–308.
Booth, J. L., and Siegler, R. S. (2006). Developmental and individual differences in pure numerical estimation. Dev. Psychol. 41, 189–201.
Boucart, M., and Humphreys, G. W. (1994). Attention to orientation, size, luminance, and color: attention failure within the form domain. J. Exp. Psychol. Hum. Percept. Perform. 20, 61–80.
Bryce, D., Szucs, D., Soltész, F., and Whitebread, D. (2011). The development of inhibitory control: an averaged and single-trial lateralized readiness potential study. Neuroimage 57, 723–732.
Case, R., and Griffin, S. (1990). “Child cognitive development: the role of central conceptual structures in the development of scientific and social thought,” in Developmental Psychology: Cognitive, Perceptuo-Motor, and Neuropsychological Perspectives, ed. C. A. Hauert (Amsterdam: Elsevier Science), 193–230.
De Smedt, B., Verschaffel, L., and Ghesquiere, P. (2009). The predictive value of numerical magnitude comparison for individual differences in mathematics achievement. J. Exp. Child Psychol. 103, 469–479.
Dehaene, S. (1997). The Number Sense: How the Mind Creates Mathematics. London: Allen Lane, The Penguin Press.
Dehaene, S., Bossini, S., and Giraux, P. (1993). The mental representation of parity and number magnitude. J. Exp. Psychol. 122, 376–396.
Dehaene, S., and Cohen, L. (1995). Towards an anatomical and functional model of number processing. Math. Cogn. 1, 83–120.
Dehaene, S., Dehaene-Lambertz, G., and Cohen, L. (1998). Abstract representations of numbers in the animal and human brain. Trends Neurosci. 21, 355–361.
Dennis, S. (1992). “Stage and structure in the development of children’s spatial representations,” in The Mind’s Staircase: Exploring the Conceptual Underpinnings of Children’s Thought and Knowledge, ed. R. Case (Hillsdale, NJ: Erlbaum), 229–246.
Ebersbach, M., Luwel, K., Frick, A., Onghena, P., and Verschaffel, L. (2008). The relationship between the shape of the mental number line and familiarity with numbers in 5- to 9-year old children: evidence for a segmented linear model. J. Exp. Child Psychol. 99, 1–17.
Feigenson, L., Spelke, E., and Carey, S. (2002). Infants discrimination of number versus continuous extent. Cogn. Psychol. 44, 33–66.
Fias, W., and Fischer, M. H. (2005). “Spatial representation of numbers,” in Handbook of Mathematical Cognition, ed. J. I. D. Campbell (New York: Psychology Press), 43–54.
Fischer, M. H., Castel, A. D., Dodd, A. D., and Pratt, J. (2003). Perceiving numbers causes spatial shifts of attention. Nat. Neurosci. 6, 555–556.
Fuson, K. C., and Briars, D. J. (1990). Using a base-ten blocks learning/teaching approach for first-and second-grade place-value and multidigit addition and subtraction. J. Res. Math. Educ. 21, 80–206.
Geary, D. C. (1994). Children’s Mathematical Development: Research and Practical Applications. Washington: American Psychological Association.
Gebuis, T., Cohen Kadosh, R., and de Haan, E. (2009). Automatic quantity processing in 5-year olds and adults. Cogn. Process. 10, 133–142.
Gelman, R., and Gallistel, C. R. (1978). The Young Child’s Understanding of Number. New York: Harvard University Press.
Girelli, L., Lucangeli, D., and Butterworth, B. (2000). The development of automaticity in accessing number magnitude. J. Exp. Child Psychol. 76, 104–122.
Griffin, S. (2004). Building number sense with number worlds: a mathematics program for young children. Early Child. Res. Q. 19, 173–180.
Griffin, S. (2005). “Fostering the development of whole-number sense: teaching mathematics in the primary grades,” in How Students Learn: History, Mathematics and Science in the Classroom, eds M. S. Donovan, and J. D. Bransford (Washington, DC: The National Academies Press), 257–308.
Griffin, S., and Case, R. (1996). Evaluating the breadth and depth of training effects when central conceptual structures are taught. Monogr. Soc. Res. Child Dev. 61, 83–102.
Griffin, S., Case, R., and Capodilupo, A. (1995). “Teaching for understanding: the importance of central conceptual structures in the elementary mathematics curriculum,” in Teaching for Transfer: Fostering Generalization in Learning, eds A. McKeough, I. Lupert, and A. Marini (Hillsdale, NJ: Erlbaum), 121–151.
Henik, A., and Tzelgov, J. (1982). Is three greater than five: the relation between physical and semantic size in comparison tasks. Mem. Cognit. 10, 389–395.
Holloway, I. D., and Ansari, D. (2008). Domain-specific and domain-general changes in children’s development of number comparison. Dev. Sci. 11, 644–649.
Holloway, I. D., and Ansari, D. (2009). Mapping numerical magnitudes onto symbols: the numerical distance effect and individual differences in children’s mathematics achievement. J. Exp. Child Psychol. 103, 17–29.
Kaufmann, L., and Nuerk, H. C. (2006). Interference effects in a numerical Stroop paradigm in 9- to 12-year-old children with ADHD-C. Child Neuropsychol. 12, 223–243.
Landerl, K., and Kölle, C. (2009). Typical and atypical development of basic numerical skills in elementary school. J. Exp. Child Psychol. 103, 546–565.
Moyer, R. S., and Landauer, T. K. (1967). Time required for judgements of numerical inequality. Nature 215, 1519–1520.
Mussolin, C., and Noël, M.-P. (2007). The nonintentional processing Arabic numbers in children. J. Clin. Exp. Neuropsychol. 29, 225–234.
Okamoto, Y., and Case, R. (1996). Exploring the microstructure of children’s central conceptual structures in the domain of number. Monogr. Soc. Res. Child Dev. 61, 27–58.
Resnick, L. B. (1983). “A developmental theory of number understanding,” in The Development of Mathematical Thinking, ed. H. P. Ginsburg (New York: Academic), 110–153.
Rousselle, L., and Noël, M. P. (2007). Basic numerical skills in children with mathematics learning disabilities: a comparison of symbolic vs. non-symbolic number magnitude processing. Cognition 102, 361–395.
Rousselle, L., and Noël, M. P. (2008). The development of automatic numerosity processing in preschoolers: evidence from numerosity-perceptual interference. Dev. Psychol. 44, 544–560.
Rubinsten, O., Henik, A., Berger, A., and Shahar-Shalev, S. (2002). The development of internal representations of magnitude and their association with Arabic numerals. J. Exp. Child Psychol. 81, 74–92.
Schneider, M., Grabner, R. H., and Paetsch, J. (2009). Mental number line, number line estimation, and mathematical achievement: their interrelations in grades 5 and 6. J. Educ. Psychol. 101, 359–372.
Schwarz, W., and Ischebeck, A. (2003). On the relative speed account of number-size interference in comparative judgments of numerals. J. Exp. Psychol. Hum. Percept. Perform. 29, 507–522.
Sekuler, R., and Mierkiewicz, D. (1977). Children’s judgments of numerical inequalities. Child Dev. 48, 630–633.
Shaki, S., Fischer, M. H., and Petrusic, W. M. (2009). Reading habits for both words and numbers contribute to the SNARC effect. Psychon. Bull. Rev. 16, 328–331.
Siegler, R. S., and Booth, J. L. (2004). Development of numerical estimation in young children. Child Dev. 75, 428–444.
Siegler, R. S., and Opfer, J. E. (2003). The development of numerical estimation: evidence for multiple representations of numerical quantity. Psychol. Sci. 14, 237–243.
Siegler, R. S., and Robinson, M. (1982). “The development of numerical understanding,” in Advances in Child Development and Behaviour, Vol. 16, eds H. W. Reese, and L. P. Lipsitt (New York: Academic), 242–312.
Soltész, F., Szücs, D., and Szücs, L. (2010). Relationships between magnitude representation, counting and memory in 4- to 7-year-old children: A developmental study. Behav. Brain Funct. 6, 1–14.
Soltész, F., White, S., and Szücs, D. (2011). Event-related brain potentials dissociate the developmental time-course of automatic numerical magnitude analysis and cognitive functions during the first three years of primary school. Dev. Neuropsychol. 36, 682–701.
Szücs, D., and Soltész, F. (2007). Event-related potentials dissociate facilitation and interference effects in the numerical Stroop paradigm. Neuropsychologia 45, 3190–3202.
Szücs, D., Soltész, F., Jarmi, E., and Csepe, V. (2007). The speed of magnitude processing and executive functions in controlled and automatic number comparison in children: an electro-encephalography study. Behav. Brain Funct. 3, 1–20.
Szűcs, D., Soltész, F., Bryce, D., and Whitebread, D. (2009). Real-time tracking of motor response activation and response competition in a Stroop task in young children: a lateralized readiness potential study. J. Cogn. Neurosci. 21, 2195–2206.
Tzelgov, J., and Ganor-Stern, D. (2005). “Automaticity in processing ordinal information,” in Handbook of Mathematical Cognition, ed. J. I. D. Campbell (New York: Psychology Press), 55–66.
Tzelgov, J., Meyer, J., and Henik, A. (1992). Automatic and intentional processing of numerical information. J. Exp. Psychol. Learn. Mem. Cogn. 18, 166–179.
van Dijck, J.-P., and Fias, W. (2011). A working memory account for spatial-numerical associations. Cognition 119, 114–119.
van Galen, M., and Reitsma, P. (2008). Developing access to number magnitude: a study of the SNARC effect in 7- to 9-year-olds. J. Exp. Child Psychol. 101, 99–113.
van Opstal, F., Gevers, W., de Moor, W., and Verguts, T. (2008). Dissecting the symbolic distance effect: comparison and priming effects in numerical and nonnumerical orders. Psychon. Bull. Rev. 15, 419–425.
van Opstal, F., and Verguts, T. (2011). The origins of the numerical distance effect: the same-different task. J. Cogn. Psychol. 23, 112–120.



